RU beehive logo ITEC dept promo banner
ITEC 380
2019spring
ibarland

home—lectures—recipe—exams—hws—D2L—breeze (snow day)

U4 shadowing, function-application; prolog

Due Apr.25 (Thu) in class Apr.26 (Fri) 23:59. Submit all files on D2L, plus hardcopy of any (parts of) files you added for U3/U4. Your prolog queries can be inside a comment of a racket file, at the top of your submitted hardcopy, thanks!

Point values will be changed somewhat, for some problems.

We continue to build on the language implementation of U1/U2. You can implement this homework in either Java or Racket. You may use the provided U2 solution if you want. Please add a comment “>>> U3” or “>>> U4” next to places you add/update for this homework. You don’t need to turn in any hardcopy of unchanged-code (but submit a fully-working copy in the drop-box). Please put new tests into the list “tests” in the U4-test file, as possible/appropriate.

    U3 is just like U2, except we now allow one variable to shadow another.

    For example, we might have a let x get … for … which in turn contains another let x get … for … inside of it. In that case the inner x should shadow the outer one:
    let x get 3 for let x get 5 for [x add 3] ⇒ let x get 5 for [x add 3]1 ⇒ [5 add 3] ⇒ 8. And of course, shadowing may occur between non-adjacent scopes: let x get 3 for (let y get 4 for (let x get 5 for …)).

    In technical terms: when substituting, only substitute “free occurrences” of an Id in E1, not any “bound occurrences”2.

    As an example, for the expression let x get 3 for (let y get 4 for [x add (let x get 5 for [x add y])]), you’d give the tree drawn at 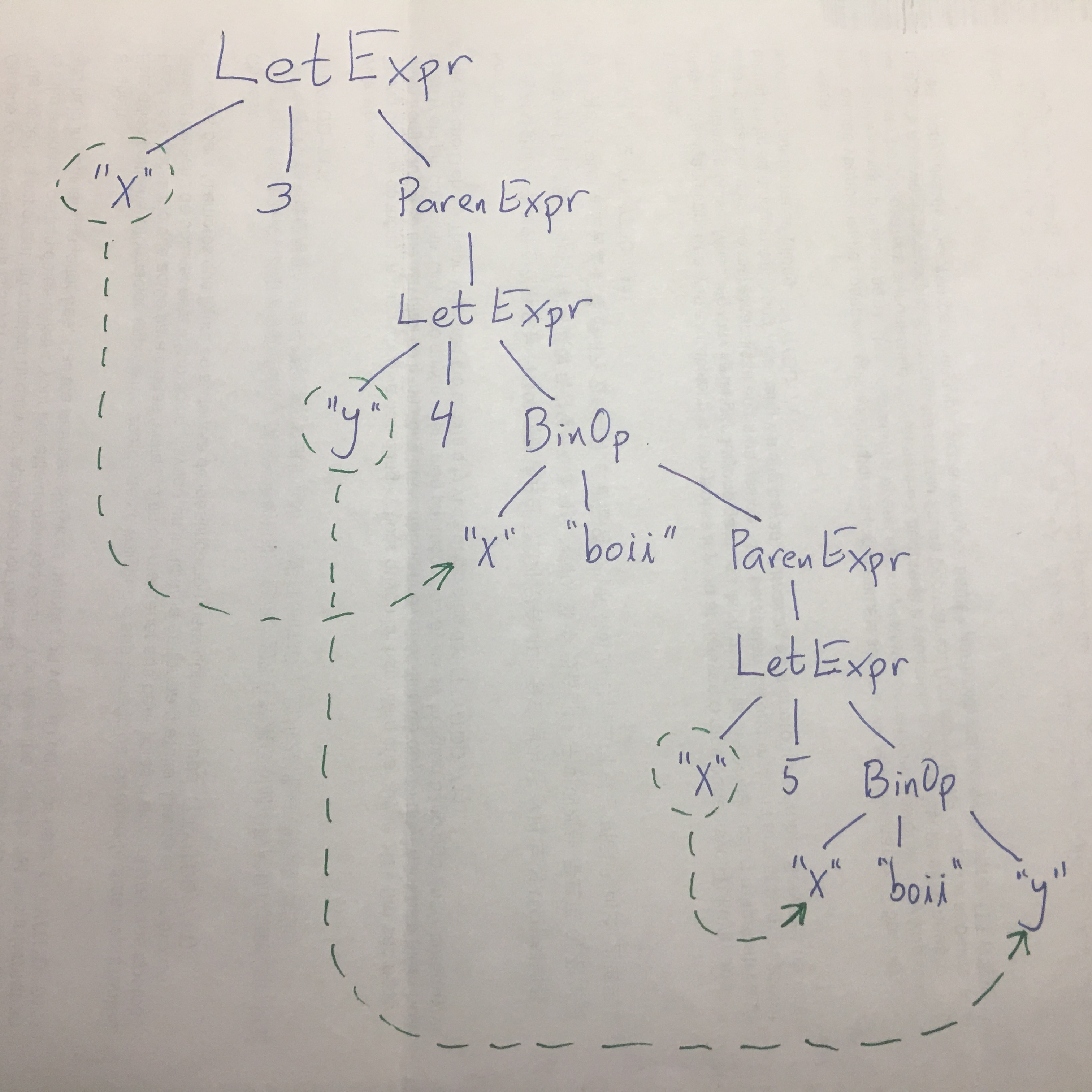abstract syntax tree, with bindings identified the right. This corresponds to some runnable test-cases: 

    (check-expect (eval (parse! "let x get 3 for (let y get 4 for [x add (let x get 5 for [x add y])])"))
              (+ 3 (+ 5 4)))
(check-expect (subst "x" 3 (parse! "(let y get 4 for [x add (let x get 5 for [x add y])])")) 
              (parse! "(let y get 4 for [3 add (let x get 5 for [x add y])])"))
    Our goal in doing this is to understand: when substituting free variables, exactly when do we stop and not substitute it in various sub-trees? For example, in the provided image: Why does the top-level "x" bind to the "x" in the middle, but not the "x" in the bottom-right? What rule can you use, when substituting, about precisely where to stop substituting? You might find it helpful to try to explain (in English) to a friend, exactly when you do and don’t substitute.

    1. (0pts) Change the purpose-statement of subst to be “substitute any free occurrences of …”. Note that you will not substitute other binding occurrences, either.
    2. For each of the following, fill in the blanks by replacing the outermost LetExpr with just its body, but substituting its variable respecting shadowing.
      For example (using the program/image above): let x get 3 for (let y get 4 for [x add (let x get 5 for [x add y])])
      ⇒ (let y get 4 for [3 add (let x get 5 for [x add y])])
      ⇒ [3 add (let x get 5 for [x add 4])]
      ⇒ [3 add ([5 add 4])] ⇒ 12.
      Complete the blanks in a similar way, below:
      1. let y get 3 for let x get 5 for [x add y] ⇒                    ⇒            ⇒ 8
      2. let y get 3 for let x get y for [x add y] ⇒                                ⇒            ⇒ 6
      3. let x get 5 for let y get 3 for [ let x get y for [x add y] add x ] ⇒                                                              ⇒                                          ⇒                      ⇒            ⇒ 11
      4. let x get 5 for (let x get [x add 1] for [x add 2]) ⇒ (let      get [     add 1] for [     add 2]) ⇒ (let      get      for [     add 2]) ⇒ ([     add 2]) ⇒ (    )

    3. (5pts) Update U2 to U3, by the necessary changes to enable shadowing.
      You are encouraged to build on your own previous solution, but you may also use the U2 solution (posted).

      • The change should be quite small, but is surgically precise.
      • Recall that U2’s subst is essentially the same code as change-name in AncTrees.
        Hint: What is needed for U3’s (and U4’s) subst is essentially the same as brown->green/stop-at-red.
      • Please label each section of lines you change with a comment “;>>>U3”.

    U4 adds (non-recursive) functions and function-application to our language: 
    Expr ::= … | FuncExpr | FuncApplyExpr

FuncExpr ::= fnc Id --> Expr
FuncApplyExpr ::= app Expr wth Expr
    Be sure not to confuse functions with function-application (calling a function) — it’s the difference between square-root (as a function), and the square-root-function-applied-to-4 (or put differently: it’s the difference between a hammer, and hitting something with a hammer).

    Here is the function (λ (x) (+ (* 3 x) 1)) written in U4: fnc x --> [[x mlt 3] add 1].
    And, here is the collatz function in U4: 

    fnc n --> iph n evn thn [[x mlt 3] add 1] els [n mlt 0.5] hpi

    Just as numbers are self-evaluating, so are FuncExprs. Evaluating (an internal representation of) a function results in that same (internal representation of the) function. We won’t actually evaluate the body until the function is applied. (This is exactly how Java, racket, python, javascript, etc. treat functions.)

    A FuncApplyExpr represents calling a function. Here are two expressions, both evaluating to 1+5·3 = 16: 

    let tripleAndInc 
get fnc x --> [[x mlt 3] add 1]
for app tripleAndInc wth 5

app fnc x --> [[x mlt 3] add 1] wth 5
    In FuncApplyExpr, the first Expr had better evaluate to a function. (That is, it might be a FuncExpr, or an Id which gets substitued to a function value. It could also be (say) an ParityExpr or LetExpr which evaluates to a function.)

    1. First, write the following four functions as U4 programs. (You can then modify them as part of your tests.)
      1. A constant function that always returns (say) 17.
      2. the function sqr, which squares its input; give it a name with a U4 LetExpr whose body we’ll just leave as “…”. I.e. write the U4 equivalent of racket (let {[sqr (lambda (x) (* x ))]} …).
      3. the factorial function, written in U4 using a LetExpr with body “…” as in the previous example.
        Note: You won’t able to evaluate function-applications for recursive functions yet (see U5), but we can still write the test cases! (You can comment out that one test case for now, since it’ll trigger a run-time exception otherwise.)
        4. and
      4. The U4 equivalent of the following racket definition make-adder: 
        (define (make-adder n)
  (lambda (m) (+ n m)))

; Two examples of applying this function:
;
(make-adder 3)     ; evals to (lambda (m) (+ 3 m))
((make-adder 3) 4) ; evals to 7
      Then, upgrade U3 so that it allows functions to be represented; label each section of lines you change with a comment “;>>>U4”.
      1. (2pts) Add a struct/class for representing FuncExprs internally.
      2. (2pts) parse! (and tests).
      3. (2pts) expr->string (and tests)
      4. (2pts) eval (and tests)
    2. Implement function-application.
      1. (2pts) Add a struct/class for representing FuncApplyExprs internally.
      2. (2pts) parse! (and tests)
      3. (2pts) expr->string (and tests)
      4. (9pts) eval (and tests). Here, more than half the points are for tests, since you want to try several situations involving shadowing variables. (You don’t need to test eval’ing your factorial function, though.)

        The semantics of eval’ing the function-application app Expr0 wth Expr1:

        1. Evaluate Expr0; let’s call the result f. (f had better be a function-value!)
        2. Evaluate Expr1; let’s call the result actual-arg.
        3. Substitute f’s parameter with actual-arg in f’s body; call this new expression E′.
        4. Evaluate E′ and return that value.
        Hey, those semantics are practically the same as LetExpr’s! Indeed, it’s not very different; the function holds the identifier and body; when you eval a function-application then we do the same substitution.

Prolog

As mentioned: Your prolog queries can be inside a comment of a (racket) file, at the top of your submitted hardcopy, thanks! Only include your added rules/facts, not the rest of the provided .pl file.

  1. (1pt) Add another super-person (hero, villain, or neither) and at least three more color-or-fighting preferences to the Prolog superhero knowledge base from lecture.
  2. (3pts) Two super-people are compatible if they share a fighting style, or a color-preference (and they aren’t the same person).
    1. define a rule compatible(A,B).
    2. What query will solve for every super-person compatible with bubbles?

  3. (5pts) Write friendly: We say two super-people are friendly if they are connected through some chain of compatible people. For example, bubbles and rafael would be friendly if compatible(bubbles,magikarp), compatible(magikarp,spongebob), and compatible(spongebob,rafael). (That is: friendly is the transitive closure of the compatible relation.) Everybody, of course, is trivially friendly with themselves (since they’re connected by a chain of 0 compatible others).

  4. (5pts) Prolog lists This problem is deferred to the next homework.

    Write the following Prolog predicates. Do not use append. For full credit, give idiomatic Prolog (no singleton variables, and no = on the right-hand-side).

    1. (3pts) last(List, Item), which succeeds exactly when Item is the last item in List. This rule should fail if List is empty, of course. (This happens to be the book’s Chpt.16, programming exercise #6.)
    2. (3pts) reverseLastTwo(List, NewList) succeeds exactly when NewList is exactly the same as List except that the last two items have been reversed. (This rule will fail if either input has fewer than two items.)
    All of the predicates fail if the first argument is not a list. Some examples (test cases) are provided, below.

    Note that the Prolog standard library contains several list functions which you are NOT to use for this assignment (e.g. append and reverse). Also, for full credit, don’t merely reverse the input list and operate on that result.

    As ever, your program should follow good style, including appropriate white space, meaningful variable names, and as well as a header comment with your name, the name of the assignment, etc.. (You can have comments describing how a predicate works if you want; however, you can also assume your program is being read by somebody who understands the fundamentals of Prolog.)

The interpreter project is based on the first chapters of Programming Languages and Interpretation, by Shriram Krishnamurthi. As a result, this homework assignment is covered by the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 United States License. Although we’re using a different dialect of racket than that book, you might find it helpful to skim it.

1 The notation “let x get 5 for (x plus 3) ⇒ 5 plus 3 ⇒ 8” is shorthand for 
  eval(parse("let x get 5 for (x plus 3)"))
= eval(parse("(5 plus 3)"))
= eval(parse("8"))
Observe how we definitely don’t write “"let x get 5 for (x plus 3)" = "(5 plus 3)" = 8” since the two strings are not .equals(·) to each other, and besides strings are never ints. More specifically: we distinguish between “⇒” (“code evaluates to”) and “=” (“equals”, just as “=” has meant since kindergarten).      ↩
2 nor any “binding occurrences”: The first x in let x get 5 for [x add 3] is a binding occurrence, and the second x is a bound occurrence. (We say that “a variable is bound inside the scope of its binding occurrence”.)      ↩

home—lectures—recipe—exams—hws—D2L—breeze (snow day)

logo for creative commons by-attribution license
This page licensed CC-BY 4.0 Ian Barland
Page last generated 		Please mail any suggestions
(incl. typos, broken links)
to ibarlandradford.edu		 Rendered by Racket.