ITEC 380 2022spring ibarland

home—lectures—recipe—exams—hws—D2L—zoom (snow day)

Shadowing and function-application
hw08: A4

Due 2022-Apr-16 (Sat) 23:59

• Please add a comment “;>>> A3” or “;>>> A4” next to places you add/update for this homework.
• You can add all new tests to the list “all-tests” in the A4-test.rkt (or, ExprTest.java).
• On D2L, submit all files except those provided with A0. (E.g. either A4,-test.rkt, or if using Java then {Expr{,Test},BinOp,IfPos,Id,Let,Func,FuncApply}.java. No .zip/.jar).

We continue to build on the language implementation of A1/A2. You can implement this homework in either Java or Racket. You may use the A2-soln if you want.If you can't see it because you didn't yet submit A2, just let me know and I'll give you access.

A3 is just like A2, except we now allow one variable to shadow another.

For example, we might have a use x | … => … which in turn contains another use x | … => … somewhere inside of it. In that case the inner x should shadow the outer one:
⇒ use x | 3 => use x | 5 => ~sum x 3
⇒ use x | 5 => ~sum x 3¹
⇒ ~sum 5 3
⇒ 8.
And of course, shadowing may occur between non-adjacent scopes: use x | 3 => use y | 4 => use x | 5 => ….

In technical terms: when substituting, only substitute “free occurrences” of an Id in E₁, not any “bound occurrences”².

As an example, for the expression use x | 3 => /use y | 4 => ~sum x /use x | 5 => ~sum x y\\, we have the syntax tree drawn at 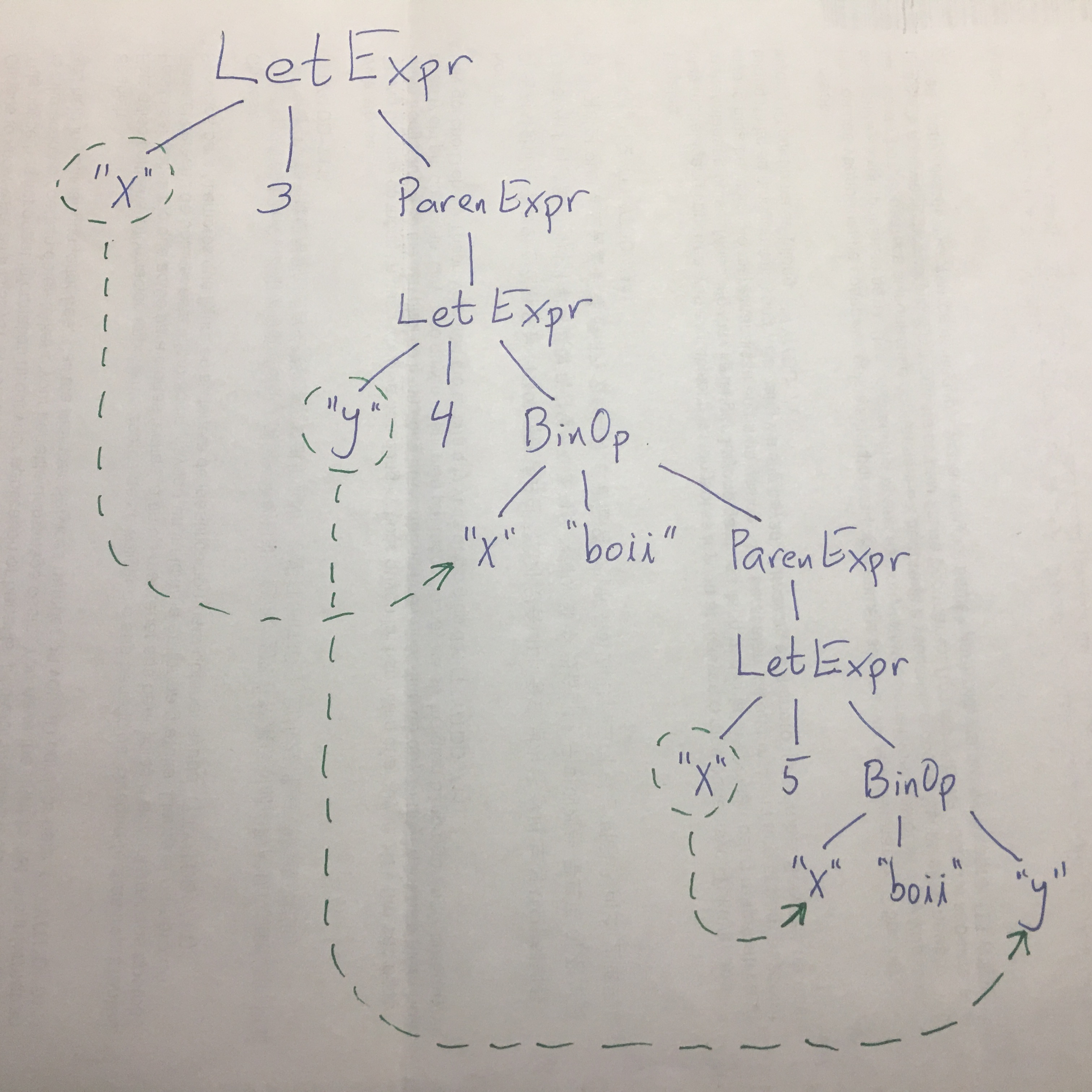the right albeit with add instead of boii, with a dotted-arrow from each binding-occurrence to its bound occurrence(s). This corresponds to some runnable test-cases³:

(check-expect (eval (string->expr "use x | 3 => /use y | 4 => ~sum x /use x | 5 => ~sum x y\\"))
              (+ 3 (+ 5 4)))
(check-expect (subst "x" 3        (string->expr "/use y | 4 => ~sum x /use x | 5 => ~sum x y\\"))
              (string->expr                     "/use y | 4 => ~sum 3 /use x | 5 => ~sum x y\\"))

hint/spoiler: in use zed | Expr_initialize => Expr_body, we know that

zed can never occur free in Expr_body. We don't even need to look inside it!

0. (0pts) Change the purpose-statement of subst to be “substitute any free occurrences of …”. Note that you will not substitute other binding occurrences, either.
1. For each of the following, fill in the blanks by replacing the outermost LetExpr with just its body, but substituting its variable respecting shadowing. You don't need to submit this, but filling it out is meant to help you understand the problem/issue. If you don't get the code working, but do have a comment with these answers, I can use them to justify partial credit!
   For example (using the program/image above):
   ⇒ use x | 3 => /use y | 4 => ~sum x /use x | 5 => ~sum x y\\
   ⇒ /use y | 4 => ~sum 3 /use x | 5 => ~sum x y\\
   ⇒ /~sum 3 /use x | 5 => ~sum x 4\\
   ⇒ /~sum 3 /~sum 5 4\\
   ⇒ 12
   Complete the blanks in a similar way, below:
   1. ⇒ use y | 3 => use x | 5 => ~sum x y
      ⇒                                             
      ⇒                         
      ⇒ 8
   2. ⇒ use y | 3 => use x | y => ~sum x y
      ⇒                                                               
      ⇒                         
      ⇒ 6
   3. ⇒ use x | 5 => use y | 3 => ~sum use x | y => ~sum x y x
      ⇒                                                                                                                           
      ⇒                                                                                     
      ⇒                                             
      ⇒                         
      ⇒ 11
   4. ⇒ use x | 5 => use x | ~sum x 1 => ~sum x 2
      ⇒ use      | ~sum      1 => ~sum      2
      ⇒ use      |      => ~sum      2
      ⇒ ~sum      2
      ⇒     

2. Update A2 to A3, by the necessary changes to enable shadowing.
   You are encouraged to build on your own previous solution, but you may also use the A2-soln (.rkt)

   • The change should be quite small, but is surgically precise.
   • Recall that A2's subst is essentially the same code as change-name in AncTrees.
     Hint: What is needed for A3's (and A4's) subst is like a anc-tree's change-name, but it stops when it reaches the name it’s changing.
   • Please label each section of lines you change with a comment “;>>>A3”.

Expr ::= … | FuncExpr | FuncApplyExpr  ;>>>A4

FuncExpr ::= lam Id => Expr            ;>>>A4   Interpretation: function-value; the Id is the parameter, and the Expr is the function's body.
FuncApplyExpr ::= app Expr ( Expr)    ;>>>A4   Interpretation: call the function (first Expr), passing it an argument (2nd Expr).

Here is the function (λ (x) (+ (* 3 x) 1)) written in A4: lam x => ~sum ~prd x 3 1.
And, here is the (uniterated) collatz function in A4:

lam n => zro ~mod n 2 ? ~prd n 0.5 : ~sum ~prd 3 n 1

Just as numbers are self-evaluating, so are FuncExprs. Evaluating (an internal representation of) a function results in that same (internal representation of the) function. We won’t actually evaluate the body until the function is applied. (This is exactly how Java, racket, python, javascript, etc. treat functions.)

A FuncApplyExpr represents calling a function. Here are two expressions, both evaluating to 5·3+1 = 16:

use tripleAndInc                       bind the name tripleAndInc…
|  lam x => ~sum ~prd x 3 1          …to a function-value
=>  app tripleAndInc ( 5 )             …and then apply it to 5

app lam x => ~sum ~prd x 3 1 ( 5 )   Equivalently: apply a function-literal

3. First, write the following four functions as A4 programs not as racket programs -- you'll write words like lam and mul. (You can later modify them to make test-cases for your A4 interpreter.)
   1. A constant function that always returns (say) 17.
   2. the function sqr, which squares its input; give it a name with a A4 LetExpr whose body we’ll just leave as “…”. I.e. write the A4 equivalent of racket (let {[sqr (lambda (x) (* x x))]} …).
   3. the factorial function, written in A4 using a LetExpr with body “…” as in the previous example.

      Note: You won’t be able to evaluate function-applications for recursive functions yet (see A5), but we can still write the test cases! (You can comment out that one test case for now, since it’ll trigger a run-time exception otherwise.)

   and
   4. The A4 equivalent of the following racket defining and calling make-adder:

      (define (make-adder n) (lambda (m) (+ n m))) ((make-adder 3) 4) ; evals to 7 ; Note that `(make-adder 3)` evals to `(lambda (m) (+ 3 m))` ; the `((` means we have *two* function-applications: ; we first call `make-adder` (getting back a lambda-value), ; then we call that result we got back.

4. Then, upgrade A3 so that it allows functions to be represented; label each section of lines you change with a comment “;>>>A4”.
   1. Add a struct/class for representing FuncExprs internally.
   2. parse! (and tests).
   3. expr->string (and tests)
   4. eval (and tests)
5. Implement function-application.
   1. Add a struct/class for representing FuncApplyExprs internally.
   2. parse! (and tests)
   3. expr->string (and tests)
   4. eval (and tests). Here, more than half the points are for tests, since you want to try several situations involving shadowing variables. (You don’t need to test eval’ing your factorial function, though.)

      The semantics of eval’ing the function-application app Expr₀ ( Expr₁):

      1. Evaluate Expr₀; let’s call the result actual-arg.
      2. Evaluate Expr₁; let’s call the result f. (f had better be a function-value!)
      3. Substitute f’s parameter with actual-arg in f’s body; call this new expression E′.
      4. Evaluate E′ and return that value.
      Hey, those semantics are practically the same as LetExpr’s! Indeed, it’s not very different; the function holds the identifier and body; when you eval a function-application then we do the same substitution.

The interpreter project is based on the first chapters of Programming Languages and Interpretation, by Shriram Krishnamurthi. As a result, this homework assignment is covered by the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 United States License. Although we’re using a different dialect of racket than that book, you might find it helpful to skim it.

  eval(string->expr("use x | 5 => ~sum x 3"))
= eval(string->expr("~sum 5 3"))
= eval(string->expr("8"))

home—lectures—recipe—exams—hws—D2L—zoom (snow day)

This page licensed CC-BY 4.0 Ian Barland Page last generated

Please mail any suggestions (incl. typos, broken links) to ibarlandradford.edu