RU beehive logo promo banner for Computing & Info Sciences
ITEC 380
2023spring
ibarland

home—lectures—recipe—hws—exams—D2L—zoom (snow day)

Shadowing and function-application
hw09: D4

Due 2023-Apr-22 (Sat) 23:59

We continue to build on the language implementation of D1/D2. You can implement this homework in either Java or Racket. You may use the D2-soln if you want. Link is usuable once you D2L-submit D2; just let me know if you need to bypass that.

D3 is just like D2, except we now allow one variable to shadow another.

For example, we might have a bind x to … in … which in turn contains another bind x to … in … somewhere inside of it. In that case the inner x should shadow the outer one:
⇒ bind x to 7 in bind x to 5 in ring x bearer 3 frodo
⇒ bind x to 5 in ring x bearer 3 frodo1
⇒ ring 5 bearer 3 frodo
⇒ 8.
And of course, shadowing may occur between non-adjacent scopes: bind x to 3 in bind y to 4 in bind x to 5 in ….

So what does our interpreter need to do? Well, when eval does substitution in a LetExpr, we just need to be a bit cautious: If we're substituting every x in an Expr, and we encounter a bind x to Exprrhs in Exprbody then we shouldn't substitute any xs inside the Exprbody. Though of course, if we encounter a bind y to Exprrhs in Exprbody, then this doesn't affect our substitution.

Using our programming-language vocabulary: when substituting, only substitute “free occurrences” of an Id in E1, not any “bound occurrences”2.

As an example, for the expression bind x to 3 in o bind y to 4 in ring x bearer o bind x to 5 in ring x bearer y frodo o frodo o, we have the syntax tree drawn at 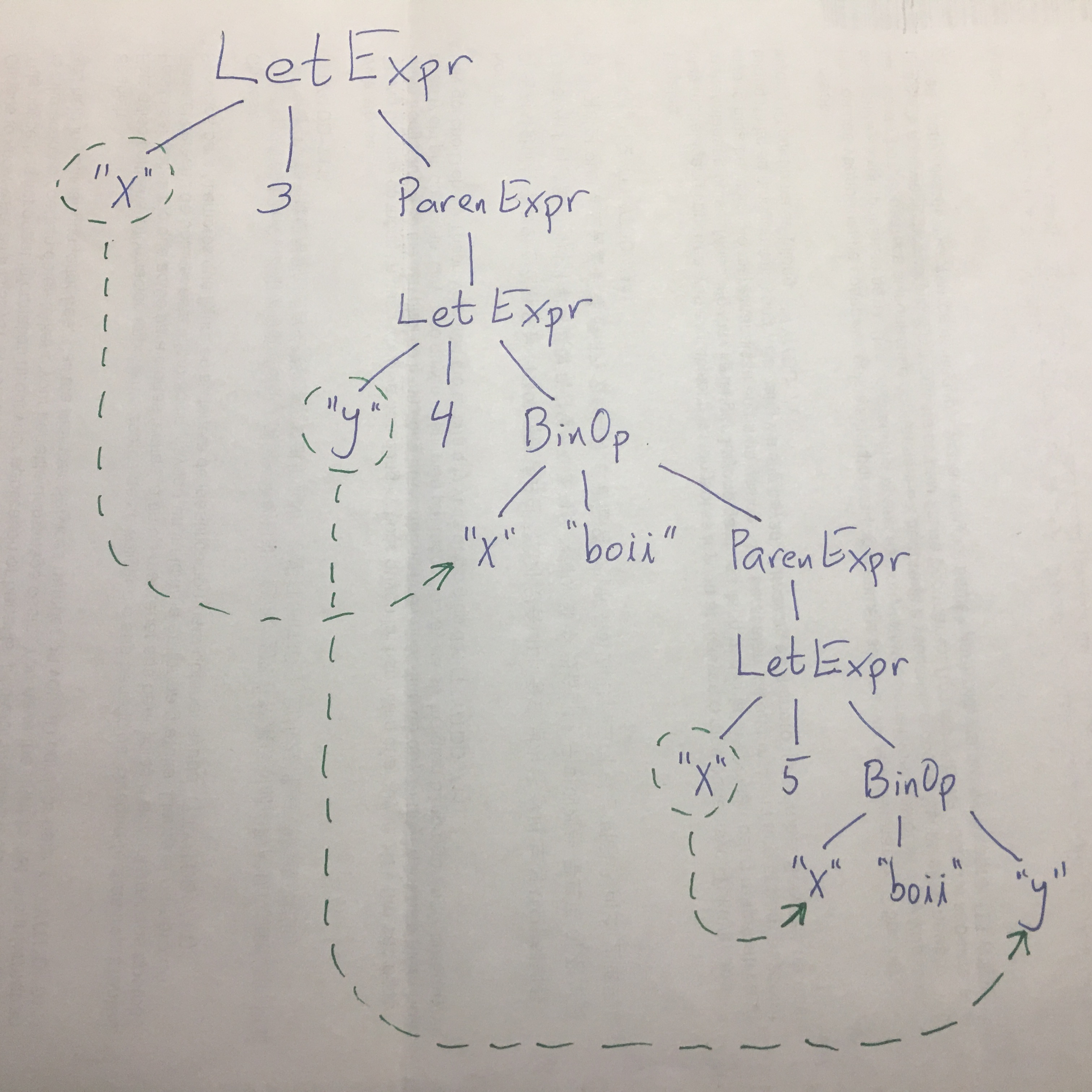abstract syntax tree, with bindings identified the right albeit with frodo written as boii, with a dotted-arrow from each binding-occurrence to its bound occurrence(s). This corresponds to some runnable test-cases3: 

(check-expect (eval (string->expr "bind x to 3 in o bind y to 4 in ring x bearer o bind x to 5 in ring x bearer y frodo o frodo o"))
              (+ 3 (+ 5 4)))
(check-expect (subst "x" 3        (string->expr "o bind y to 4 in ring x bearer o bind x to 5 in ring x bearer y frodo o frodo o"))
              (string->expr                     "o bind y to 4 in ring 3 bearer o bind x to 5 in ring x bearer y frodo o frodo o"))
Our goal in doing this is to understand: when substituting free variables, exactly when do we stop and not substitute it in various sub-trees? For example, in the provided image: Why does the top-level x bind to the x in the middle, but not the x in the bottom-right? What rule can you use, when substituting, about precisely where to stop substituting?
hint/spoiler: in bind zed to Exprinitialize in Exprbody, we know that
zed can never occur free in Exprbody. We don't even need to look inside it!

  1. (0pts) Change the purpose-statement of subst to be “substitute any free occurrences of …”. Note that you will not substitute other binding occurrences, either.
  2. For each of the following, fill in the blanks by replacing the outermost LetExpr with just its body, but substituting its variable respecting shadowing. You don't need to submit this, but filling it out is meant to help you understand the problem/issue. If you don't get the code working, but do have a comment with these answers, I can use them to justify partial credit!
    For example (using the program/image above):
    ⇒ bind x to 3 in o bind y to 4 in ring x bearer o bind x to 5 in ring x bearer y frodo o frodo o
    ⇒ o bind y to 4 in ring 3 bearer o bind x to 5 in ring x bearer y frodo o frodo o
    ⇒ o ring 3 bearer o bind x to 5 in ring x bearer 4 frodo o frodo o
    ⇒ o ring 3 bearer o ring 5 bearer 4 frodo o frodo o
    ⇒ 12
    Complete the blanks in a similar way, below:
    1. ⇒ bind y to 3 in bind x to 5 in ring x bearer y frodo
      ⇒                                             
      ⇒                                                               
      ⇒ 8
    2. ⇒ bind y to 3 in bind x to y in ring x bearer y frodo
      ⇒                                                                                                             
      ⇒                                                               
      ⇒ 6
    3. ⇒ bind x to 5 in bind y to 3 in ring bind x to y in ring x bearer y frodo bearer x frodo
      ⇒                                                                                                                                                                                                                     
      ⇒                                                                                                                                                                         
      ⇒                                                                                                                           
      ⇒                                                               
      ⇒ 11
    4. ⇒ bind x to 5 in bind x to ring x bearer 1 frodo in ring x bearer 2 frodo
      ⇒ bind      to ring      bearer 1 frodo in ring      bearer 2 frodo
      ⇒ bind      to      in ring      bearer 2 frodo
      ⇒ ring      bearer 2 frodo
      ⇒     

  3. Update D2 to D3, by the necessary changes to enable shadowing.
    You are encouraged to build on your own previous solution, but you may also use the D2-soln (.rkt)

D4 adds (non-recursive) functions and function-application to our language: 
Expr ::= … | FuncExpr | FuncApplyExpr  ;>>>D4

FuncExpr ::= forge Id into Expr            ;>>>D4   Interpretation: function-value; the Id is the parameter, and the Expr is the function's body.
FuncApplyExpr ::= wield Expr against Expr    ;>>>D4   Interpretation: apply the function (first Expr) to the argument (2nd Expr).
Be sure not to confuse functions with function-application (calling a function) — it’s the difference between square-root (as a function), and the square-root-function-applied-to-4 (or put differently: it’s the difference between a hammer, and hitting something with a hammer).

Here is the function (λ (x) (+ (* 3 x) 1)) written in D4: forge x into ring ring x bearer 3 samwise bearer 1 frodo.
And, here is the (uniterated) collatz function, (λ(n) (if (even? n) (* n 1/2) (+ (* 3 n) 1))), written in D4: 

forge n into for ring n bearer 2 sauron gondor ring n bearer 0.5 samwise ring ring 3 bearer n samwise bearer 1 frodo

Just as numbers are self-evaluating, so are FuncExprs. Evaluating (an internal representation of) a function results in that same (internal representation of the) function. We won’t actually evaluate the body until the function is applied. (This is exactly how Java, racket, python, javascript, etc. treat functions.)

A FuncApplyExpr represents calling a function. Here are two expressions, both evaluating to 5·3+1 = 16: 

bind tripleAndInc
to   forge x into ring ring x bearer 3 samwise bearer 1 frodo      body of `tripleAndInc`
in   wield tripleAndInc against 5     call tripleAndInc(5)… 


wield forge x into ring ring x bearer 3 samwise bearer 1 frodo against 5   Equivalently: apply a function-literal (w/o bothering to give it a name)
In FuncApplyExpr, the first Expr had better evaluate to a function. (That is, it might be a FuncExpr, or an Id which gets substitued to a function value. It could also be (say) an ParityExpr or LetExpr which evaluates to a function.)

  1. First, write the following four functions as D4 programs not as racket programs -- you'll write keywords like forge and ring. They'll just be in comments since they're not racket code. Or hey, you can put them in a string, and then pass those strings to parse as test-cases!.
    1. A constant function that always returns (say) 17.
    2. the function sqr, which squares its input; give it a name with a D4 LetExpr whose body we’ll just leave as “…”. I.e. write the D4 equivalent of racket (let {[sqr (lambda (x) (* x x))]} …).
    3. the factorial function, written in D4 using a LetExpr with body “…” as in the previous example.
      Note: You won’t be able to evaluate function-applications for recursive functions yet (see D5), but we can still write the test cases! (You can comment out that one test case for now, since it’ll trigger a run-time exception otherwise.)
      4. and
    4. The D4 equivalent of the following racket defining and calling make-adder: 
      (define (make-adder n)
  (lambda (m) (+ n m)))

((make-adder 3) 4) ; evals to 7

; Note that `(make-adder 3)` evals to `(lambda (m) (+ 3 m))`
; the `((` means we have *two* function-applications:
; we first call `make-adder` (getting back a lambda-value),
; then we call that result we got back.
  2. Then, upgrade D3 so that it allows functions to be represented; label each section of lines you change with a comment “;>>>D4”.
    1. Add a struct/class for representing FuncExprs internally.
    2. parse! (and tests).
      heads-up: The provided racket and java parsers each return a punctuation-character as a single token. So when parsing “<=” you'll need to pop twice to consume both punctuation-characters.
    3. expr->string (and tests)
    4. eval (and tests)
  3. Implement function-application.
    1. Add a struct/class for representing FuncApplyExprs internally.
    2. parse! (and tests)
    3. expr->string (and tests)
    4. eval (and tests). Here, more than half the points are for tests, since you want to try several situations involving shadowing variables. (You don’t need to test eval’ing your factorial function, though.)

      The semantics of eval’ing the function-application wield Expr0 against Expr1:

      1. Evaluate Expr0Expr1; let’s call the result actual-arg.
      2. Evaluate Expr1Expr0; let’s call the result f. (f had better be a function-value!)
      3. Substitute f’s parameter with actual-arg in f’s body; call this new expression E′.
      4. Evaluate E′ and return that value.
      Hey, those semantics are practically the same as LetExpr’s! Indeed, it’s not very different; the function holds the identifier and body; when you eval a function-application then we do the same substitution.

Prolog

Your prolog queries can be inside a comment of a (racket) file, at the top of your submitted hardcopy, thanks! Only include your added rules/facts, not the rest of the provided .pl file.

  1. Prolog: basic queries.
    1. Add another super-person (hero, villain, or neither) and at least three more color-or-weapon preferences to the Prolog superhero knowledge base from lecture. Use the site swish.swi-prolog.org/
    2. Two super-people are compatible if they share a fighting style, or a color-preference (and they aren’t the same person). Moreover, team(A,B,C) is true if A and B are compatible, and B and C are compatible, but A and C aren’t the same.
      1. define a rule compatible(A,B).
      2. What query will solve for every super-person compatible with bubbles?
      3. define team(A,B,C).
      4. What query will solve for every team starting with bubbles and ending with rafael?
    Note: Put our prolog queries inside a comment of a (racket) file, at the top of your submitted hardcopy, thanks! Only include your added rules/facts, not the rest of the provided .pl file.

  2. Prolog paths (transitive closure): Continuing from defining compatible in the previous problem, write friendly:
    We say two super-people are friendly if they are connected through some chain of compatible people. For example, bubbles and rafael would be friendly if compatible(bubbles,magikarp), compatible(magikarp,squirtle), and compatible(squirtle,rafael). (That is: friendly is the reflexive, transitive closure of the compatible relation.) Everybody, of course, is trivially friendly with themselves (since they’re connected by a chain of 0 compatible others).

    Note:

    It's okay if you get infinite loops:
    Since there can be cycles of friendly people (unlike our ancestor example), prolog (which uses depth-first search, rather than breadth-first), can get into infinite loops! In particular, asking friendly(bubbles,some_person_who_isnt_friendly_w_bubbles) can trigger an infinite loop. Asking friendly(bubbles,X) will give you back the same solutions repeatedly. (But asking about two people who are friendly should work just fine.) We'll just ignore such loops, for this homework.

    (Fwiw: the general solution would be to either (a) add an “exclusion” list of people already tried4, or (b) use datalog, a restricted version of prolog which uses BFS, and is always guaranateed to terminate (See #lang racklog, in racket), or (c) add

    We're using prolog to learn about the mindset of declarative programming (and its cool pattern-matching/unification) — I'm not interested in us learning about the details of prolog's internal algorithms.

The interpreter project is based on the first chapters of Programming Languages and Interpretation, by Shriram Krishnamurthi. As a result, this homework assignment is covered by the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 United States License. Although we’re using a different dialect of racket than that book, you might find it helpful to skim it.

1 The notation “bind x to 5 in ring x bearer 3 frodo ⇒ ring 5 bearer 3 frodo ⇒ 8” is shorthand for 
  eval(string->expr("bind x to 5 in ring x bearer 3 frodo"))
= eval(string->expr("ring 5 bearer 3 frodo"))
= eval(string->expr("8"))
Observe how we definitely don’t write “"bind x to 5 in ring x bearer 3 frodo" = "ring 5 bearer 3 frodo" = 8” since the two strings are not .equals(·) to each other, and besides strings are never ints. More specifically: we distinguish between “⇒” (“code evaluates to”) and “=” (“equals”, just as “=” has meant since kindergarten).      ↩
2 nor any “binding occurrences”: The first x in bind x to 5 in ring x bearer 3 frodo is a binding occurrence, and the second x is a bound occurrence. (We say that “a variable is bound inside the scope of its binding occurrence”.)      ↩
3 Blue x represents a binding-occurrence; x is a bound occurrence; x is a free occurrence.      ↩
4 The XSB implementation of prolog can use memoization (“tabling”) to avoid re-calling a query on a node already called. In fact, Dr. Uppuluri worked on this system, as a graduate student!      ↩

home—lectures—recipe—hws—exams—D2L—zoom (snow day)

logo for creative commons by-attribution license
This page licensed CC-BY 4.0 Ian Barland
Page last generated 		Please mail any suggestions
(incl. typos, broken links)
to ibarlandradford.edu		 Rendered by Racket.