ITEC 380 2024spring ibarland

home—lectures—recipe—hws—exams—D2L—zoom (snow day)

Shadowing and function-application
hw09: F4

Due Apr.18 (Thu) start of class19 (Fri) 23:59

• Please add a comment “;>>> F3” or “;>>> F4” next to places you add/update for this homework.
• You can add all new tests to the list “all-tests” in the F4-test.rkt (or, ExprTest.java).
• On E2L, submit all files except those provided with F0. (E.g. either F4,-test.rkt, or if using Java then {Expr{,Test},BinOp,IfPos,Id,Let,Func,FuncApply}.java. No .zip/.jar).

We continue to build on the language implementation of F1/F2. You can implement this homework in either Java or Racket. You may use the F2-soln if you want. Link is usuable once you E2L-submit F2; just let me know if you need to bypass that.

F3 is just like F2, except we now allow one variable to shadow another.

For example, we might have a moon x on … eclipses … which in turn contains another moon x on … eclipses … somewhere inside of it. In that case the inner x should shadow the outer one:
⇒ moon x on 7 eclipses moon x on 5 eclipses tilt x sum 3
⇒ moon x on 5 eclipses tilt x sum 3¹
⇒ tilt 5 sum 3
⇒ 8.
And of course, shadowing may occur between non-adjacent scopes: moon x on 3 eclipses moon y on 4 eclipses moon x on 5 eclipses ….

So what does our interpreter need to do? Well, when eval does substitution in a LetExpr, we just need to be a bit cautious: If we're substituting every x in an Expr, and we encounter a moon x on Expr_rhs eclipses Expr_body then we shouldn't substitute any xs inside the Expr_body. Though of course, if we encounter a moon y on Expr_rhs eclipses Expr_body, then this doesn't affect our substitution.

Using our programming-language vocabulary: when substituting, only substitute “free occurrences” of an Id in E₁, not any “bound occurrences”².

As an example, for the expression moon x on 3 eclipses (moon y on 4 eclipses tilt x sum (moon x on 5 eclipses tilt x sum y)), we have the syntax tree drawn at 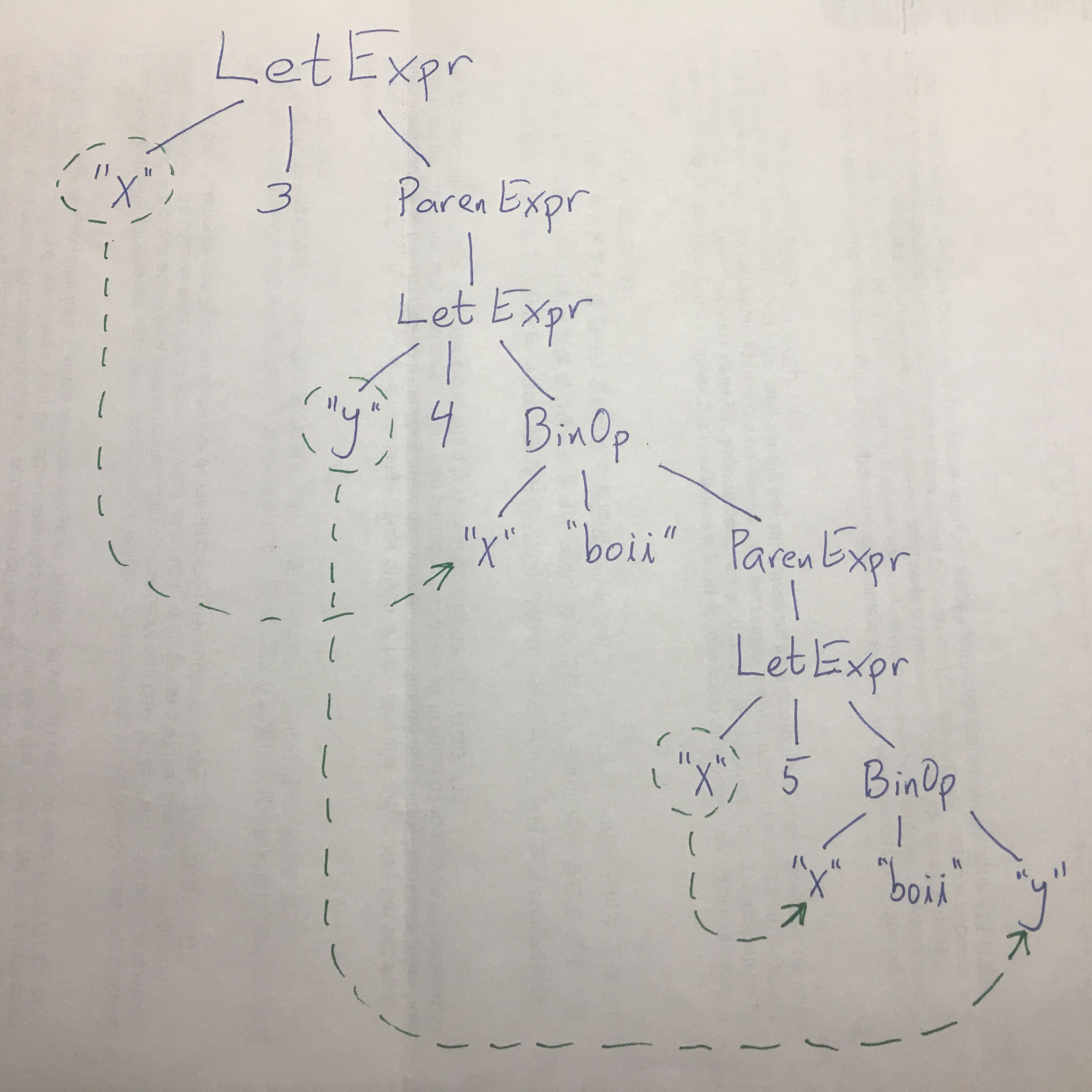the right albeit with sum written as boii, with a dotted-arrow from each binding-occurrence to its bound occurrence(s). This corresponds to some runnable test-cases³:

(check-expect (eval (string->expr "moon x on 3 eclipses (moon y on 4 eclipses tilt x sum (moon x on 5 eclipses tilt x sum y))"))
              (+ 3 (+ 5 4)))
(check-expect (subst "x" 3        (string->expr "(moon y on 4 eclipses tilt x sum (moon x on 5 eclipses tilt x sum y))"))
              (string->expr                     "(moon y on 4 eclipses tilt 3 sum (moon x on 5 eclipses tilt x sum y))"))

hint/spoiler: in moon zed on Expr_initialize eclipses Expr_body, we know that

zed can never occur free in Expr_body

. We don't even need to look inside it, if we are only looking for free occurrences of (a surrounding) zed!

0. (0pts) Change the purpose-statement of subst to be “substitute any free occurrences of …”. Note that you will not substitute other binding occurrences, either.
1. For each of the following, fill in the blanks by replacing the outermost LetExpr with just its body, but substituting its variable respecting shadowing. You don't need to submit this, but filling it out is meant to help you understand the problem/issue. If you don't get the code working, but do have a comment with these answers, I can use them to justify partial credit!
   For example (using the program/image above):
   ⇒ moon x on 3 eclipses (moon y on 4 eclipses tilt x sum (moon x on 5 eclipses tilt x sum y))
   ⇒ (moon y on 4 eclipses tilt 3 sum (moon x on 5 eclipses tilt x sum y))
   ⇒ (tilt 3 sum (moon x on 5 eclipses tilt x sum 4))
   ⇒ (tilt 3 sum (tilt 5 sum 4))
   ⇒ 12
   Complete the blanks in a similar way, below:
   1. ⇒ moon y on 3 eclipses moon x on 5 eclipses tilt x sum y
      ⇒                                             
      ⇒                                     
      ⇒ 8
   2. ⇒ moon y on 3 eclipses moon x on y eclipses tilt x sum y
      ⇒                                                                                                   
      ⇒                                     
      ⇒ 6
   3. ⇒ moon x on 5 eclipses moon y on 3 eclipses tilt moon x on y eclipses tilt x sum y sum x
      ⇒                                                                                                                                                                                                   
      ⇒                                                                                                                                     
      ⇒                                                                     
      ⇒                                     
      ⇒ 11
   4. ⇒ moon x on 5 eclipses moon x on tilt x sum 1 eclipses tilt x sum 2
      ⇒ moon      on tilt      sum 1 eclipses tilt      sum 2
      ⇒ moon      on      eclipses tilt      sum 2
      ⇒ tilt      sum 2
      ⇒     

2. Update F2 to F3, by the necessary changes to enable shadowing.
   You are encouraged to build on your own previous solution, but you may also use the F2-soln (.rkt)

   • The change should be quite small, but is surgically precise.
   • Recall that F2's subst is essentially the same code as change-name in AncTrees.
     Hint: What is needed for F3's (and F4's) subst is essentially the same as exam01's workers-follow-queen-color.
   • Please label each section of lines you change with a comment “;>>>F3”.

F4 adds (non-recursive) functions and function-application to our language:

Expr → … | FuncExpr | <FuncApplyExpr>     ;>>>F4

FuncExpr → orbit Id aroundExpr              ;>>>F4   Interpretation: function-value; the Id is the parameter, and the Expr is the function's body.
FuncApplyExpr → launch Expr into Expr   ;>>>F4   Interpretation: apply the function (first Expr) to the argument (2nd Expr).

Here is the function (λ (x) (+ (* 3 x) 1)) written in F4: orbit x around tilt tilt x spr 3 sum 1.
And, here is the (uniterated) collatz function, (λ(n) (if (even? n) (* n 1/2) (+ (* 3 n) 1))), written in F4:

orbit n around if tilt n fall 2 equinox tilt n spr 0.5 : tilt tilt 3 spr n sum 1

A FuncApplyExpr represents calling a function. Here are two expressions, both evaluating to 5·3+1 = 16:

moon tripleAndInc
on   orbit x around tilt tilt x spr 3 sum 1          body of `tripleAndInc`
eclipses   launch tripleAndInc into 5            call tripleAndInc(5)… 


launch orbit x around tilt tilt x spr 3 sum 1 into 5   Equivalent to above: apply a function-literal (w/o bothering to give it a name)

3. First, write the following four functions as F4 programs not as racket programs -- you'll write keywords like orbit and tilt. They'll just be in comments since they're not racket code. Or hey, you can put them in a string, and then pass those strings to parse as test-cases!.
   1. A constant function that always returns (say) 17.
   2. the function sqr, which squares its input; give it a name with a F4 LetExpr whose body we’ll just leave as “…”. I.e. write the F4 equivalent of racket (let {[sqr (lambda (x) (* x x))]} …). If you like, you can aply the function to 5, instead of writing “…”. That might make things clearer, but on the other hand it involves the syntax for function-creation and function-application, which is why I it's optional.
   3. the factorial function, written in F4 using a LetExpr with body “…” as in the previous example.

      Note: You won’t be able to evaluate function-applications for recursive functions yet (see F5), but we can still write the test cases! (You can comment out that one test case for now, since it’ll trigger a run-time exception otherwise.)

   and
   4. The F4 equivalent of the following racket defining and calling make-adder:

      (define (make-adder n) (lambda (m) (+ n m))) ((make-adder 3) 4) ; evals to 7 ; Note that `(make-adder 3)` evals to `(lambda (m) (+ 3 m))` ; the `((` means we have *two* function-applications: ; we first call `make-adder` (getting back a lambda-value), ; then we call that result we got back.

4. Then, upgrade F3 so that it allows functions to be represented; label each section of lines you change with a comment “;>>>F4”.
   1. Add a struct/class for representing FuncExprs internally.⁴
   2. parse! (and tests).

      heads-up: The provided racket and java parsers each return a punctuation-character as a single token. So when parsing “<=” you'll need to pop twice to consume both punctuation-characters.

   3. expr->string (and tests)
   4. eval (and tests).

      Semantics of a function-literal: Just as numbers are self-evaluating, so are FuncExprs. Evaluating (an internal representation of) a function results in that same (internal representation of the) function. We won’t actually evaluate the body until the function is applied. (This is exactly how Java, racket, python, javascript, etc. treat functions.)

   Testing function-values: How can we make a test-cases, when the result isn't a number? For example, for evaluating orbit n around tilt n sum 1 or launch makeAdder into 5 (whose expected-results are both <FuncExpr> structs). You have two approaches:

   • Use check-expect as usual: e.g.

     (check-expect (eval (string->expr "orbit n around tilt n sum 1")) (make-my-func-expr "n" (make-binop "sum" "n" 1)))

     This is more to write than using test-harness, but works just fine.
   • Use the test-harness: adding a <Expr>/result pair to the list-of-tests works mostly as usual, but we need one extra character: a comma, immediately preceding the expected-result. E.g.:

     ["orbit n around tilt n sum 1" ,(make-my-func-expr "n" (make-binop "sum" "n" 1))]

     [optional] Why the comma?: If you want to understand why it doesn't work without a comma, and what the comma does for us, you can read ../../Lectures/backquote.html (recommended, but not necessary to complete this homework).

     tl;dr: The test-harness's list of program+result pairs isn't created by calling list (over and over for each pair); instead it was created by using a single backquote, “`”: (define all-tests `(("tilt 2 sum 3" 5) …). This quote then distributes over all the nested open-parens to create sub-lists woo-hoo!, a handy time-saver. In fact, it also quotes the values inside those sub-lists — which didn't previously matter to us, because quoting string-literals and integer-literals has no effect ('16 is 16, and '"hello" is "hello").

     However: quoting an identifier turns it into a symbol ('hello is 'hello :-). So `(3 (sqrt 16) 5) is (list 3 (list 'sqrt 16) 5), and not (list 3 4 5) like we hoped. To suppress the quoting of (sqrt 16), we precede it with a comma: `(3 ,(sqrt 16) 5) gives (list 2 3 4). (The comma is known as unquote.)

5. Implement function-application.
   1. Add a struct/class for representing FuncApplyExprs internally.
   2. parse! (and tests)
   3. expr->string (and tests)
   4. eval (and tests). Here, more than half the points are for tests, since you want to try several situations involving shadowing variables. (You don’t need to test eval’ing your factorial function, though.)

      The semantics of eval’ing the function-application launch Expr₁ into Expr₀ launch Expr₀ into Expr₁:

      1. Evaluate Expr₀; let’s call the result f. (f had better be a function-value!)
      2. Evaluate Expr₁; let’s call the result actual-arg.
      3. Substitute f’s parameter with actual-arg in f’s body; call this new expression E′.
      4. Evaluate E′ and return that value.
      Hey, those semantics are practically the same as <LetExpr>’s! Indeed, it's just that the identifier, thing-to-substitute, and body aren't all in a single <LetExpr>; now they are divided between a <FuncExpr> and a <FuncApplyExpr>.

   external resource: Another description of this algorithm is in VT's textbook's section A Substitution-Based Model of Evaluation.

The interpreter project is based on the first chapters of Programming Languages and Interpretation, by Shriram Krishnamurthi. As a result, this homework assignment is covered by the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 United States License. Although we’re using a different dialect of racket than that book, you might find it helpful to skim it.

  eval(string->expr("moon x on 5 eclipses tilt x sum 3"))
= eval(string->expr("tilt 5 sum 3"))
= eval(string->expr("8"))

home—lectures—recipe—hws—exams—D2L—zoom (snow day)

This page licensed CC-BY 4.0 Ian Barland Page last generated

Please mail any suggestions (incl. typos, broken links) to ibarlandradford.edu