


Next: Important Questions that you
Up: No Title
Previous: Some Exercises
If 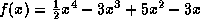 and
and 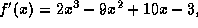 first we factor
first we factor 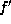 (assuming we can factor or we use "
factor(2*x^3-9*x^2+10*x-3);" in Maple to do this) into
(assuming we can factor or we use "
factor(2*x^3-9*x^2+10*x-3);" in Maple to do this) into 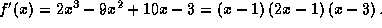 And notice that we have practiced the followings:
And notice that we have practiced the followings:
- If
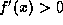 for x in (a,b), then f is increasing in (a,b), and
for x in (a,b), then f is increasing in (a,b), and
- If
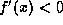 for x in (c,d), then f is decreasing in (c,d).
for x in (c,d), then f is decreasing in (c,d).
But 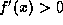 when
when 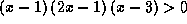 (which amounts in solving an inequality). Great, it is in
standard form, we see the answer is
(which amounts in solving an inequality). Great, it is in
standard form, we see the answer is 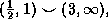 which
means that f is increasing in
which
means that f is increasing in 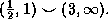
Similarly, 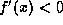 if
if 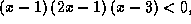 and the answer is when x is in
and the answer is when x is in 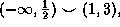 which means that f is decreaing in
which means that f is decreaing in 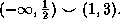
- Example 1: Suppose f'(x) = (x-1)(x-3)(x-5) (note that this
is the derivative function), then f'(x)>0 in (1,3) u (5, infinity),
which means the original function f is "increasing" in (1,3) u (5,
infinity). Morevoer, since f'(x)<0 in (-infinity, 1) u (3,5), we see that
f is decreasing in (-infinity, 1) u (3,5).
- Example 2: Suppose f'(x) = - (x-1)(x-3)(x-7) , then f'(x)>0
in (-infinity, 1) u (3,7) and hence f is increasing in those intervals.
On the other hand, f'(x)<0 in (1,3) union (7, infinity), so f is
decreasing there.
- Important Questions that you need to answer later in this class.
- Horizontal Tangent
Wei-Chi Yang
Sat Oct 19 00:19:09 EDT 1996
![]() and
and ![]() first we factor
first we factor ![]() (assuming we can factor or we use "
factor(2*x^3-9*x^2+10*x-3);" in Maple to do this) into
(assuming we can factor or we use "
factor(2*x^3-9*x^2+10*x-3);" in Maple to do this) into ![]() And notice that we have practiced the followings:
And notice that we have practiced the followings:
![]() when
when ![]() (which amounts in solving an inequality). Great, it is in
standard form, we see the answer is
(which amounts in solving an inequality). Great, it is in
standard form, we see the answer is ![]() which
means that f is increasing in
which
means that f is increasing in ![]()
![]() if
if ![]() and the answer is when x is in
and the answer is when x is in ![]() which means that f is decreaing in
which means that f is decreaing in ![]()