next up previous
Up: The Title Previous: The Title

Increasing and Decreasing Functions AND Extrema and the First derivative test

Test for increasing or decreasing functions

Let f be differentiable on the interval (a,b).

  1. If tex2html_wrap_inline153 for all x in (a,b), then f is increasing in (a,b).
  2. If tex2html_wrap_inline163 for all x in (a,b), then f is decreasing on (a,b).

Definition of a critical number

If f is defined at c, then c is a critical number of f if tex2html_wrap_inline181 or tex2html_wrap_inline183 is undefined at c.

Use of the critical numbers

  1. If x=c is a critical number of f and tex2html_wrap_inline191 then we can use the derivative of f to test if x=c is a maximum or a minimum.
  2. If x=c is a critical number of f and tex2html_wrap_inline201 is undefined, then we can use the derivative of f to test if x=c is a maximum or a minimum. Moreover, f possibly has a sharp corner or a vertical tangent at x=c.

Test for finding the relative extrema

Suppose that f has a critical number at x=c and tex2html_wrap_inline181.

  1. In the interval (a,b), if tex2html_wrap_inline163 on tex2html_wrap_inline219 and tex2html_wrap_inline153 on tex2html_wrap_inline223, then f has a relative minimum at x=c.
  2. In the interval (a,b), if tex2html_wrap_inline153 on tex2html_wrap_inline219 and tex2html_wrap_inline163 on tex2html_wrap_inline223, then f has a relative maximum at x=c.

Examples

Find the critical numbers and open intervals on which the function is increasing or decreasing.

Example: If f(x)=-2x2+4x+3 (page 180, #19). First we find tex2html_wrap_inline245 By setting tex2html_wrap_inline2 47 we find x=1, which is the critical point of f.

(1) If x>1 (say x=2), then tex2html_wrap_inline259 thus f is decreasing in tex2html_wrap_inline263

(2) If x<1 (say x=0), then tex2html_wrap_inline269 thus f is increasing in tex2html_wrap_inline273

(3) f has a relative maximum at x=1. (note the maximum point on the graph will be (1,f(1))=(1,5).)

Example: If f(x)=3x3+12x2+15x (page 180, #21). First we find tex2html_wrap_inline283 By setting tex2html_wrap_inline247 we find tex2html_wrap_inline287 and x=-1.

(1) The critical numbers are tex2html_wrap_inline287 and x=-1.

(2) The signs of tex2html_wrap_inline183 is displayed as follows: 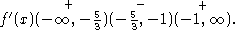tex2html_wrap_inline297Therefore, f is increasing on tex2html_wrap_inline301 and decreasing on tex2html_wrap_inline303

(3) There is a relative maximum at tex2html_wrap_inline305 and a relative minimum at x=-1. Use MFI to check your answer.

Example: If tex2html_wrap_inline309 First tex2html_wrap_inline311

Notice that h(1) is defined but tex2html_wrap_inline315 is undefined, so x=1 is a critical number of h.

If x>1, then tex2html_wrap_inline323 If x<1, then tex2html_wrap_inline323 Thus h is increasing everywhere. There is no relative extrema.

Example: If tex2html_wrap_inline331 First, tex2html_wrap_inline333 Notice that the crical numbers are at x=2 and x=3.

(1) If tex2html_wrap_inline339 say x=1, tex2html_wrap_inline343

(2) If tex2html_wrap_inline345 say x=2.5, tex2html_wrap_inline349

(3) If tex2html_wrap_inline351say x=4, tex2html_wrap_inline355 is undefined, also notice that the domain of f does not include tex2html_wrap_inline359 So we don't have graph for x>3.

Therefore, f is increasing on tex2html_wrap_inline365 and decreasing (2,3).

There is a relative maximum at x=2. Use plot(2*x*sqrt(3-x),x=-5..5, thickness=3); to obtain a plot from MFI.

Example: If tex2html_wrap_inline371 We see tex2html_wrap_inline373

Notice that the critical numbers of f are at x=-1,1; x=0 is not a critical number because f(0) is undefined even if tex2html_wrap_inline383 is undefined.

However, when we determine the sign of tex2html_wrap_inline385 we need to take x=0 into consideration. 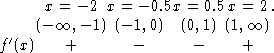tex2html_wrap_inline389

Therefore, f is increasing on tex2html_wrap_inline393 and decreasing on (-1,1).

f has a relative maximum at x=-1 (be sure that f(-1) is defined), and a relative minimum at x=1.