The left sum of a given function f over the partition defined
above is the Riemann sum 
where, for each j, the number tj is the left endpoint of
the interval that runs from 
to 
In other words, we define the left sum by pointing at t
he
equation 
and clicking on Define and New Definition. Similarly, the right sum of f is 
and we define it by pointing at the equation and
clicking on Define and New Definition. The arithmetic mean
of the left and right sums is the trapezoidal sum 
which we define by pointing at the equation
Alternatively we could observe that
and use this equation for the
definition of the trapezoidal sum. As we shall see from the examples that
follow, the trapezoidal sum is frequently a much better approximation to the
integral than either the left or the right sum. An even better approximation
than the trapezoidal sum is the midpoint sum 
which we define by pointing at the equation 
In this sum the function f is evaluated for each j at the midpoint of
the interval that runs from to
Finally, the Simpson sum 
of f over the
given partition is defined by pointing at the equation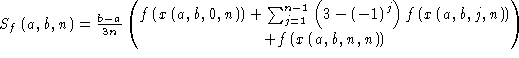 
As you may know, the Simpson sum is used only when the number n is even.