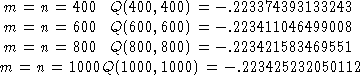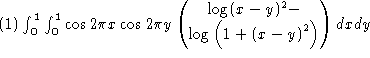
Consider evaluating the following numerical integral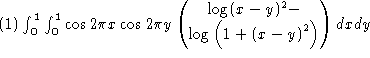 
Both Maple and Mathematica could not give an answer due the singularities lie along x=y. What we will do is to transform the singularities to the boundary first and apply a quadrature which uses uniformly regular matrices for computations.
Note that the function 
is symmetric
with respect to y=x, so we consider the integration over the triangle with
vertices O=(0,0), P=(1,0) and Q=(1,1). After the transformation with
change of variables, u=x, and v=x-y, the singular points are shifted to x- axis, and the Jacobian is 
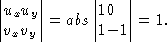Thus, equation (1) becomes
By using
the uniformly regular matrices 
and 
and write a corresponding
Pascal program, we obtain the following information
