ITEC 380 2021spring ibarland

home—lectures—recipe—exams—hws—D2L—zoom (snow day)

Interpreting Y
(as developed in lecture)

The language Y0

Y0:
Expr    ::= Num | Paren | BinOp | IfZero
Paren   ::= {= Expr =}                          Interpretation: a parenthesized expression
BinOp   ::= > Op Expr Expr <                    Interpretation: apply a binary operator
Op      ::= blam | swish | splat                Interpretation: addition, subtraction, multiplication (resp.)
IfZero  ::= bliff Expr zok Expr nooo Expr       Interpretation: if 1st-expr is 0, eval to 2nd-expr, else 3rd-expr.  Mnemonic: branch iff … zero,ok? … else if nooot: …

Y1:see Y2.html for details
Op      ::= … | pow | oof                       Interpretation: “exponentiation”, “remainder1”
Expr    ::= … | IfGT                            Interpretation: “if greater than”
IfGT    ::= glurp Expr Expr zok Expr nooo Expr  Mnemonic: greater/lesser(p)

Y2:see Y2.html for details
Expr    ::= … | Id | LetExpr                    Interpretation: identifier; let
LetExpr ::= zlott Id biff Expr @ Expr           Mnemonic: (z)let Id be(ff) … in(at) …

 
Y4:see Y4.html for details
 Expr ::= … | FuncExpr | FuncApplyExpr

 FuncExpr ::= thonk Id => Expr          Interpretation: a function-value, with parameter Id and body-Expr.
 FuncApplyExpr ::= krunch Expr <= Expr   Interpretation: apply a function (1st expr) to an argument (2nd expr)

Semantics (interpretation):

• A Paren is a parenthesized expression (used for grouping only);
• A Binop is a (prefix) binary operator expression; blam means addition; swish means subtraction (the 2nd arg from the 1st); splat means multiplication.
• A IfZero evaluates its first expressions; if it's zero then then the result is is the second expression (evaluated), else the result is the last expression (evaluated).

Discussion

• Give five example programs (Exprs) written in Y0.
• Give their parse trees.
• How should we represent these trees, internally? (In Racket, and equivalently in Java).

Where we're headed

• For interpreting this language, we will implement three methods:
  • parse, which turns source-code into an internal representation,
  • toString which turns internal representation back into source-code,
  and
  • eval, which actually interprets the program, returning a value (a number for Y0-Y2, and a number-or-function in Y3).
  I recommend implementing and testing the methods in this order. Some test-cases will be provided. There might be other helper functions to implement as well.

Y0 Implementations

• Y0.rkt, with helper files scanner.rkt (and, scanner-demo.rkt); test cases Y0-tests.rkt, and student-extras.rkt.

  Note: Download the racket files, and then choose Open… from DrRacket. Do not copy/paste into an empty DrRacket window, since that window is probably using a student-language, and some of the files below use full racket.

• Java: Y0-java/ (browse the directory), or see the .jar.
  Note the composite pattern to implement union-types, in Java: The classes Expr and its four variants Num/BinOp/IfZero/Paren are organized in the same way AncTree and its two variants Child/Unknown were.

Discuss the implementation

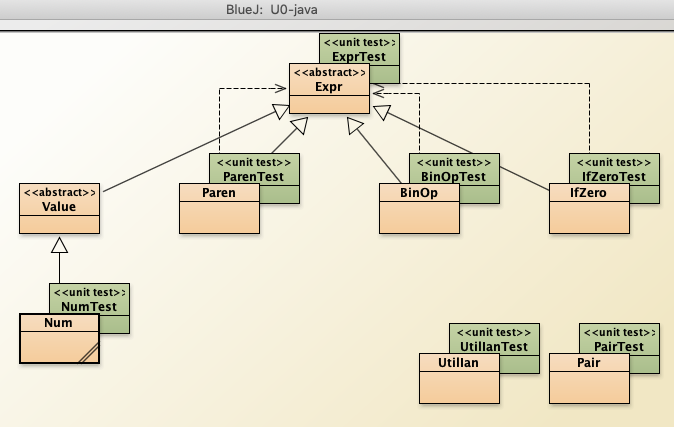
Once we've talked in class about internal-representation (and given examples of the W programs and corresponding internal-data), then we can discuss the provided-implementation, including recursive-descent parsing:

2018 version: The videos below are based on 2018fall's language, T0. So details of the syntax are different than this semester, and some statements might have different semantics, but overall the content is extremely similar to this semester's language.

• Look over expr->string, eval in Y0.rkt (or T0.rkt, the exact version from the video). The code directly follows the design recipe. video (9m13s)
  
  
• Look over the same code in Y0-java/ (or T0-java/, the exact version from the video). The code is equivalent to the racket — still just following the design recipe. video (13m04s)
  
  
• parse — recursive-descent parsing: video (17m21s)
  
  
  • It does not exactly follow the the design recipe (because it processes a string/scanner, not Exprs), yet the code's shape is still extremely correlated to the Y0 grammar/datatype-definition.
  • This is called “recursive descent” parsing.

    Note: Parsing Y0 is particularly easy because each expression-type's leading-token lets us know exactly what to expect, removing the need for look-ahead, backtracking, or cleverer algorithms.

  • The Java code is essentially the same, up to class Scanner working a bit differently. video (12m19s)
    
    .
• Optional, but helpful for your own test cases:
  • Writing test-cases the regular, same-ol’ same-ol’ way, and then realizing what we can re-factor into easier-to-write tests, via an “test-harness” specific to this assignment. In racket: video (14m14s)
    
    
  • The same test-harness, in Java (slightly more involved, and less flexible): video (8m08s)
    
    

home—lectures—recipe—exams—hws—D2L—zoom (snow day)

This page licensed CC-BY 4.0 Ian Barland Page last generated

Please mail any suggestions (incl. typos, broken links) to ibarlandradford.edu